Simulation and Modeling
Lecture notes
Lecture notes from a survey course on simulation methodologies, techniques, and applications. The main focus of this course is on the use of computer simulation in physical sciences. The goal is to gain some experience in developing both continuous system and discrete event simulations. We will discuss how to setup first-order differential equations and solve these numerically to simulate simple physical systems, such as mass-spring systems, bouncing balls, etc. Rigid body dynamics, collision detection and collision response topics will also be covered. The course will also discuss many particle systems, random processes, and schemes for verifying and validating simulations.
Faisal Qureshi
Email: faisal.qureshi@ontariotechu.ca
Web: http://vclab.science.ontariotechu.ca
Forward
Constructing computer simulations is perhaps one of the funnest things one can do with a computer. Imagine the thrill of simulating an entire planet inhabited with life-like beings going about their business, pondering life's big questions? Ok, we aren't quite there yet, but already we have access to countless games that simulate one phenomenon or another for the purposes of entertainment. Think SimCity that simulates a metropolis, or Factorio that simulates, what can only be described as, a logistics nightmare. We have games that simulate driving cars, flying airplanes, playing soccer, hunting big game, and fighting in wars, etc. Similarly we have games that simulate entire worlds populated with dinosaurs and robots and everything in-between: Xenoblade, any one.
Within this context, this course aims to introduce students to computer simulations. We will not be using simulation packages rather we will explore the mathematical models and programming practices that underpin systems that can be used to create computer simulations.
Entertainment and games are not the primary use of computer simulations however. Designers and engineers rely heavily on simulations when designing and implementing complex systems, e.g., airplanes, bridges, highways, drugs, nuclear reactors, etc. Simulations enable us to ask the what if question, which is especially useful when we do not have the access to the actual system or when it is simply too dangerous to run the experiments on the actual system. E.g., how many cars before a bridge collapses? Clearly, we cannot pile cars on a bridge and wait for it to collapse! Many a times simulation is the only mechanism through which we can study a phynomenon.
Another use of simulations is in education and training sphere where it is sometimes easier, cheaper, less dangerous to use a simulation for training. Think how pilots are routinely trained on high-fidelity flight simulators.
Within this context, we will discuss the mathematics, physics, and statistics theory plus programming practices that underpin modern computer simulations. The focus is not to use existing computer simulation tools rather the course aims at developing competency needed to implement computer simulations. By necessity we will focus on setting up simulations for toy problems, such as a ball bouncing on an inclined plane, a factory floor, nuclear decay, random walks, etc.
Notes

Building simulations
- Why simulations?
- Validate a model or a theory
- Perform experiments
- Support model-based design
- Education and training
- Building simulations
- Requirements
- Modeling
- Data collection
- Implementation
- Validation
- Use

Continuous systems
- Variables: state, input, and output
- Time
- Ordinary Differential Equations (ODEs)
- Reducibility
- Energy calculations
- Potential and kinectic energy
- Terminal Velocity
- Friction and drag
- Solving ODEs numerically
- Euler method
- Runga-Kutta method
- Many bodies simulation
- Examples
- Mass-Spring system
- Ball falling under gravity
- Bouncing balls
- Projectile motion
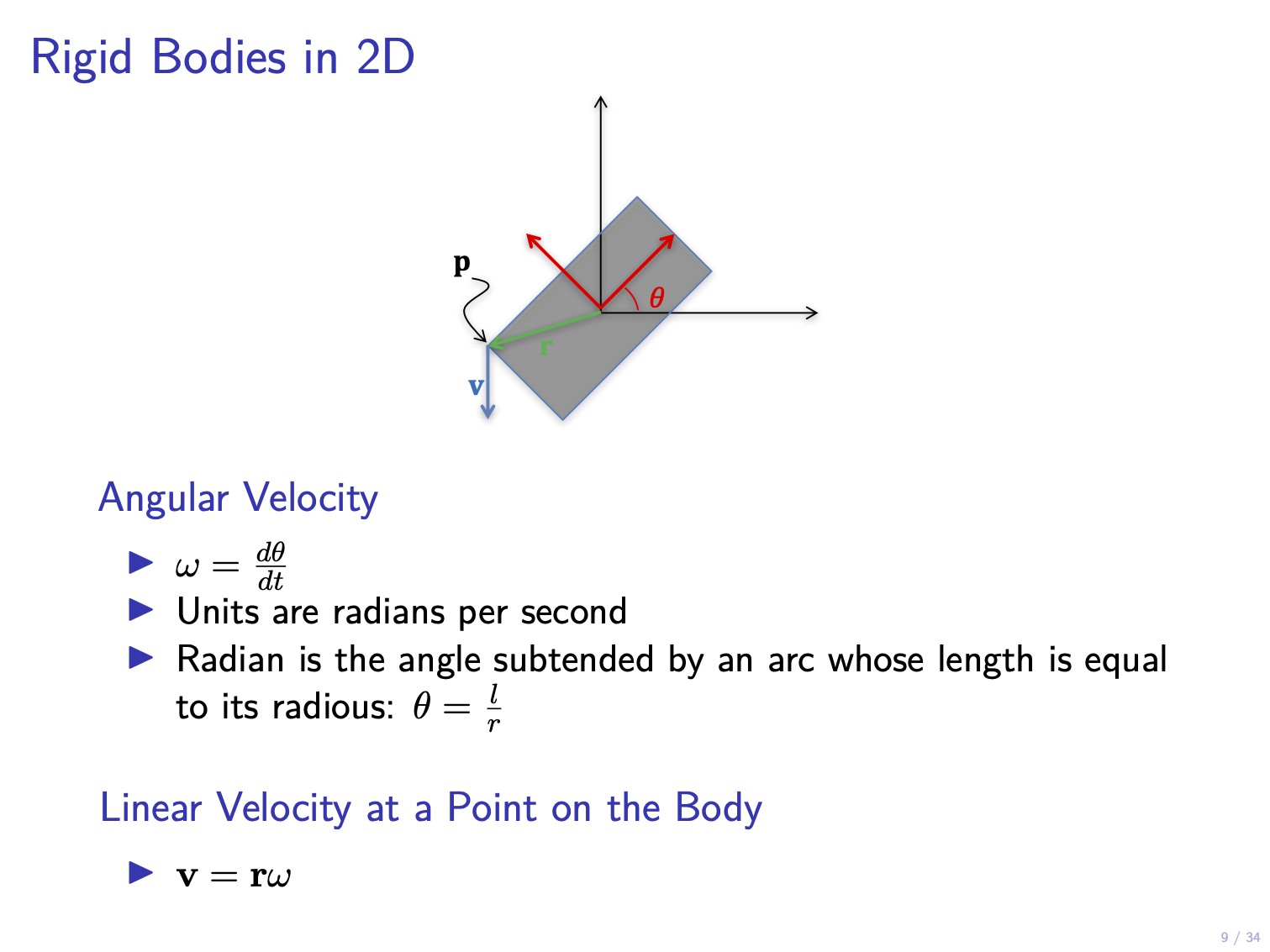
Rigid body dynamics
- Particles vs. rigid bodies
- Coordinate frames
- Linear and angular velocities
- Torque
- Center of mass
- Inertia tensor
- Equations of motions
- Shape representation

Collision detection
- Collisions with a static object
- Collision between moving targets
- Moving forward and backward in time
- Efficiency considerations
- Spatial partitioning
- Rigid body collisions
- Collision detection
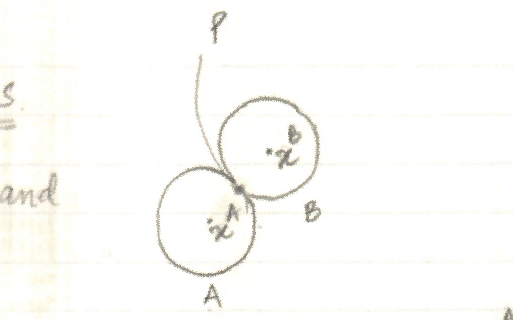
Rigid body collisions response
- Newton's Law of Restitution for Instantaneous Collision with no Friction
- Conservation of momentum
- Empirical model of frictionless collision

Random processes
- Generating random numbers
- Uniform discrete distributions
- Non-uniform discrete distributions
- Non-uniform continuous distributions
- Normal distribution
- Exponential distribution
- Random processes
- Monte Carlo simulations
- Random walks

Discrete event systems
- Anatomy of a discrete event system
- Data collection considerations
- Sensitivity analysis
- Communicating results to support decision making

Many particle systems
- Many particle systems
- Molecular dynamics
- Boundary conditions
- Setting up initial conditions
- Pressure and temperature
- Ensemble
- Microcanonical ensemble
- Quasi-ergodic hypothesis
- Demon algorithm
- Ising model

Verification and validation
- Verification
- Validation
Reference resources
Reading material
No single textbook covers all the material that we will discuss in this course. Still the following two books are useful for a deeper study of most of the topics that we will cover in this course.
- Harvey Gould, Jan Tobochnik, and Wolfgang Christian, “An Introduction to Computer Simulation Methods: Applications to Physical Systems,” Third Edition, Addison Wesley, 2007. This book is available at https://www.compadre.org/osp/items/detail.cfm?ID=7375.
- Wolfgang Christian, “Open Source Physics: A User’s Guide with Examples,” Addison Wesley, 2007.
Programming resources
- Python3
- pygame: a package for creating 2D graphics applications.
- simpy: a package for constructing discrete event simulations.
- pymunk: a package for 2D physics simulation.
- matplotlib: a package for data visualization and plotting.
Copyright and License
© Faisal Z. Qureshi

This
work is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.