Simulation and Modeling (CSCI 3010U)
Faculty of Science, Ontario Tech University
http://vclab.science.ontariotechu.ca
Check Course Canvas for Due Date
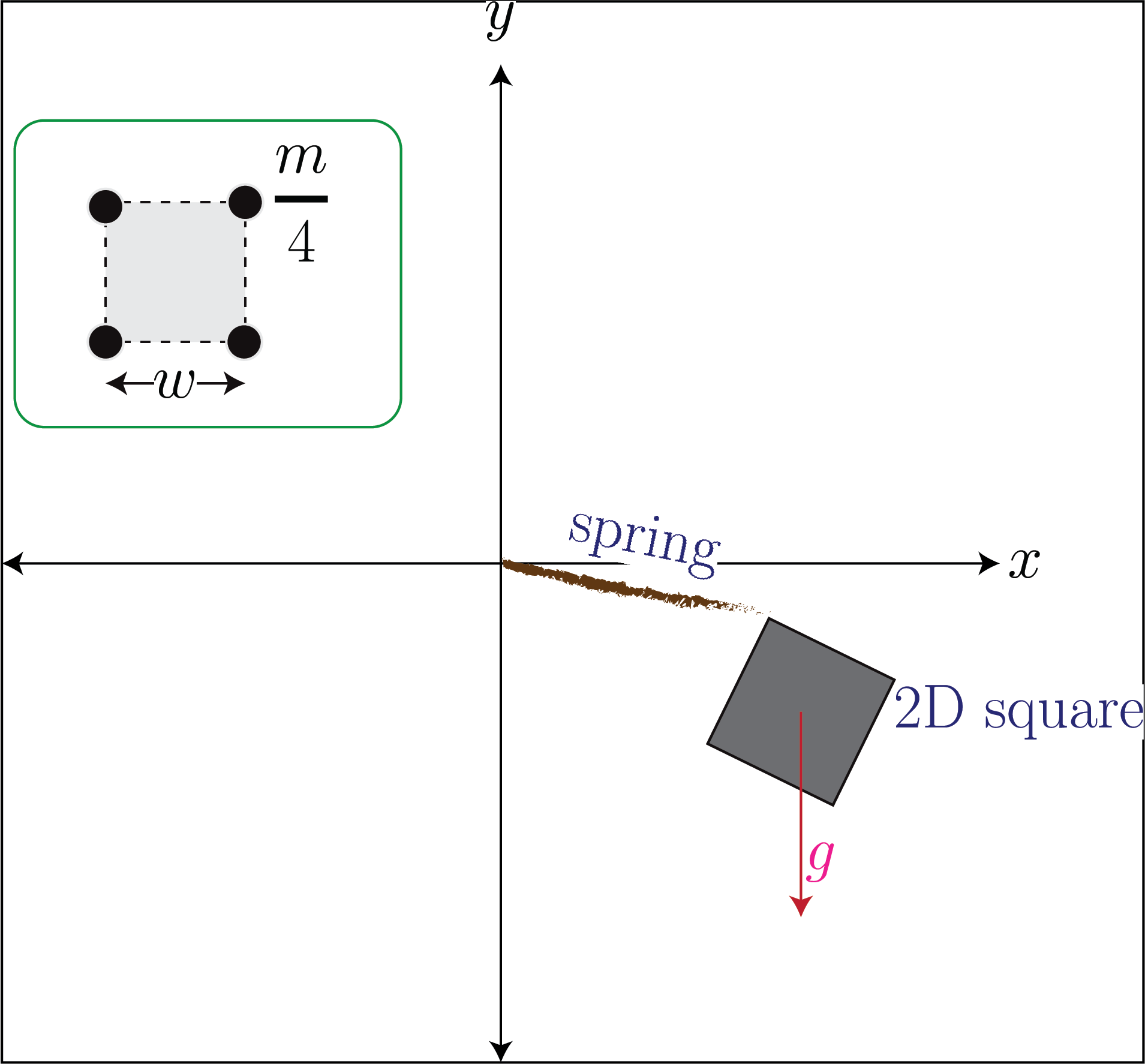
Consider the figure below that shows a 2D square connected to a spring.

Here one end of the spring is connected to one of the corners of the square, and the other end of this spring is connected to a fixed point \((0,0)\). The rest length of the spring is \(l\), and the spring constant is \(k\). As we release the square it falls under the influence of gravity \(g\) (acting along the \(-y\) direction). The square also experiences force (and torque) as the spring extends and contracts. You are asked to simulate this system. The mass of the spring is \(m\), and it is equally distributed at its four courners, i.e., mass at each corner is \(\frac{m}{4}\). Each side of the 2D square is \(w\). Let’s also assume that it is a damped spring and the damping coefficient is \(c\). Recall that the damping simply resists any motion.
You’ll need to pick your own values of the quantities of interest:
Let’s set \(g\) equal to \(9.8 m/{s^2}\).
You may use the sample code below to get things going.
"""
author: Faisal Qureshi
email: faisal.qureshi@ontariotechu.ca
website: http://www.vclab.ca
license: BSD
"""
import pygame, sys
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import ode
# set up the colors
BLACK = (0, 0, 0)
WHITE = (255, 255, 255)
RED = (255, 0, 0)
GREEN = (0, 255, 0)
BLUE = (0, 0, 255)
class RigidBody:
def __init__(self, force, torque):
self.mass = 1.0 # mass
self.Ibody = np.identity(3) # inertia tensor
self.IbodyInv = np.linalg.inv(self.Ibody) # inverse of inertia tensor
self.v = np.zeros(3) # linear velocity
self.omega = np.zeros(3) # angular velocity
self.state = np.zeros(19)
self.state[0:3] = np.zeros(3) # position
self.state[3:12] = np.identity(3).reshape([1,9]) # rotation
self.state[12:15] = self.mass * self.v # linear momentum
self.state[15:18] = np.zeros(3) # angular momentum
# Computed quantities
self.force = force
self.torque = torque
# Setting up the solver
self.solver = ode(self.f)
self.solver.set_integrator('dop853')
self.solver.set_f_params(self.force, self.torque, self.IbodyInv)
def f(self, t, state, force, torque, IbodyInv):
rate = np.zeros(19)
rate[0:3] = state[12:15] / self.mass # dv = dx/dt
_R = state[3:12].reshape([3,3])
_R = self.orthonormalize(_R)
Iinv = np.dot(_R, np.dot(IbodyInv, _R.T))
_L = state[15:18]
omega = np.dot(Iinv, _L)
rate[3:12] = np.dot(self.star(omega), _R).reshape([1,9])
rate[12:15] = force
rate[15:18] = torque
return rate
def star(self, v):
vs = np.zeros([3,3])
vs[0][0] = 0
vs[1][0] = v[2]
vs[2][0] = -v[1]
vs[0][1] = -v[2]
vs[1][1] = 0
vs[2][1] = v[0]
vs[0][2] = v[1]
vs[1][2] = -v[0]
vs[2][2] = 0
return vs;
def orthonormalize(self, m):
mo = np.zeros([3,3])
r0 = m[0,:]
r1 = m[1,:]
r2 = m[2,:]
r0new = r0 / np.linalg.norm(r0)
r2new = np.cross(r0new, r1)
r2new = r2new / np.linalg.norm(r2new)
r1new = np.cross(r2new, r0new)
r1new = r1new / np.linalg.norm(r1new)
mo[0,:] = r0new
mo[1,:] = r1new
mo[2,:] = r2new
return mo
def get_pos(self):
return self.state[0:3]
def get_rot(self):
return self.state[3:12].reshape([3,3])
def get_angle_2d(self):
v1 = [1,0,0]
v2 = np.dot(self.state[3:12].reshape([3,3]), v1)
cosang = np.dot(v1, v2)
axis = np.cross(v1, v2)
return np.degrees(np.arccos(cosang)), axis
def prn_state(self):
print('Pos', self.state[0:3])
print('Rot', self.state[3:12].reshape([3,3]))
print('P', self.state[12:15])
print('L', self.state[15:18])
class Box2d(pygame.sprite.Sprite):
def __init__(self, x, y, screen_height, imgfile):
pygame.sprite.Sprite.__init__(self)
self.image = pygame.image.load(imgfile)
self.rect = self.image.get_rect()
self.pos = (x,y)
self.image_rot = self.image
self.screen_height = screen_height
def rotate(self, angle):
self.image_rot = pygame.transform.rotate(self.image, angle)
def move(self, x, y):
new_x = self.pos[0] + x
new_y = self.pos[1] + y
self.pos = (new_x, new_y)
def draw(self, surface):
rect = self.image_rot.get_rect()
rect.center = self.pos
rect.centery = self.screen_height - rect.centery
surface.blit(self.image_rot, rect)
def main():
# initializing pygame
#pygame.mixer.init()
pygame.init()
clock = pygame.time.Clock()
# some music
#pygame.mixer.music.load('madame-butterfly.wav')
# top left corner is (0,0)
win_width = 640
win_height = 640
screen = pygame.display.set_mode((win_width, win_height))
pygame.display.set_caption('2D projectile motion')
background = pygame.image.load('background-vertical.png')
box = Box2d(320, 320, win_height, 'square.png')
box_exploded = Box2d(320, 320, win_height, 'square-exploded.png')
rb = RigidBody([0,-1,0], [0,0,0.1])
cur_time = 0.0
dt = 0.1
rb.solver.set_initial_value(rb.state, cur_time)
exploded = False
while True:
# 30 fps
clock.tick(30)
event = pygame.event.poll()
if event.type == pygame.QUIT:
pygame.quit()
sys.exit(0)
elif event.type == pygame.KEYDOWN and event.key == pygame.K_q:
pygame.quit()
sys.exit(0)
else:
pass
if not exploded:
rb.state = rb.solver.integrate(cur_time)
cur_time += dt
angle, axis = rb.get_angle_2d()
if axis[2] < 0:
angle *= -1.
pos = rb.get_pos()
# clear the background, and draw the sprites
screen.blit(background, (pos[0],pos[1]))
if pos[1] < -1600:
exploded = True
box_exploded.draw(screen)
else:
box.rotate(angle)
#box.move(pos[0], pos[1])
box.draw(screen)
pygame.display.update()
if __name__ == '__main__':
main()The assets used in this code are available here.
Also, don’t forget that this is actually a 3D simulation, with z-axis poking out of the screen. We still display it as a 2D simulation. The code provided above does just that.
Via Canvas.
This is what the simulation would look like