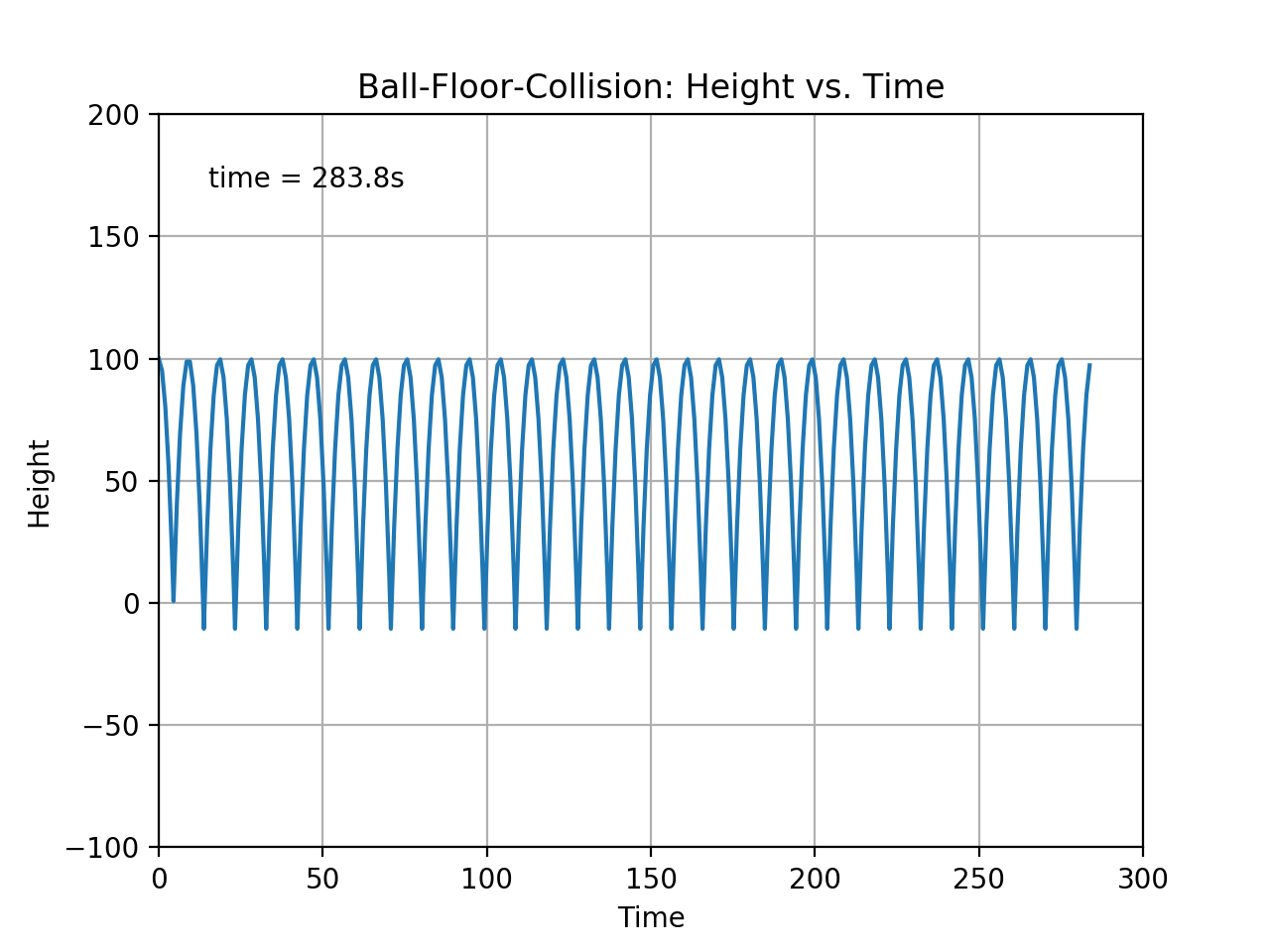
Using a large tolerance value results in the ball passing through the floor by a greater distance.
Simulation and Modeling (CSCI 3010U)
Faculty of Science, Ontario Tech University
http://vclab.science.ontariotechu.ca
Check Course Canvas for Due Date
Earlier in the course we simulated a bouncing ball. The ball would fall under the effect of gravity, hit a floor and bounce back up. There we discovered that our ball was actually penetrating the floor. We can fix this problem by using ever smaller time steps. However, this approach doesn’t work in practice. A better way is to find the exact time of collision and respond to the collision when it occurs.
The following videos suggest the importance of finding the exact collisions-time. The first video below shows how the system continues to gain energy when we allow the ball to penetrate the floor; even though we fix the graphics and show as if the ball never went below the floor.
Video 1 (Current Setup)
Video 2 (Finding Exact Collision Times)
In this lab you are asked to implement binary search to find the exact collision time of a ball with a floor at height \(0\). We assume that our ball has mass \(1\) and that it is moving under the influence of gravity (no friction, please).
We know that the floor sits at height \(0\), and we are interested in finding the exact time at which the ball is located within distance \(tol_d\) from the floor.
This \(tol_d\) enables us to control the accuracy vs. speed of our simulation. Use larger tolerance to speed up the simulation at the cost of accuracy, or lower the tolerance and get very accurate ball-floor-collisions (See the two figures below).

Using a large tolerance value results in the ball passing through the floor by a greater distance.
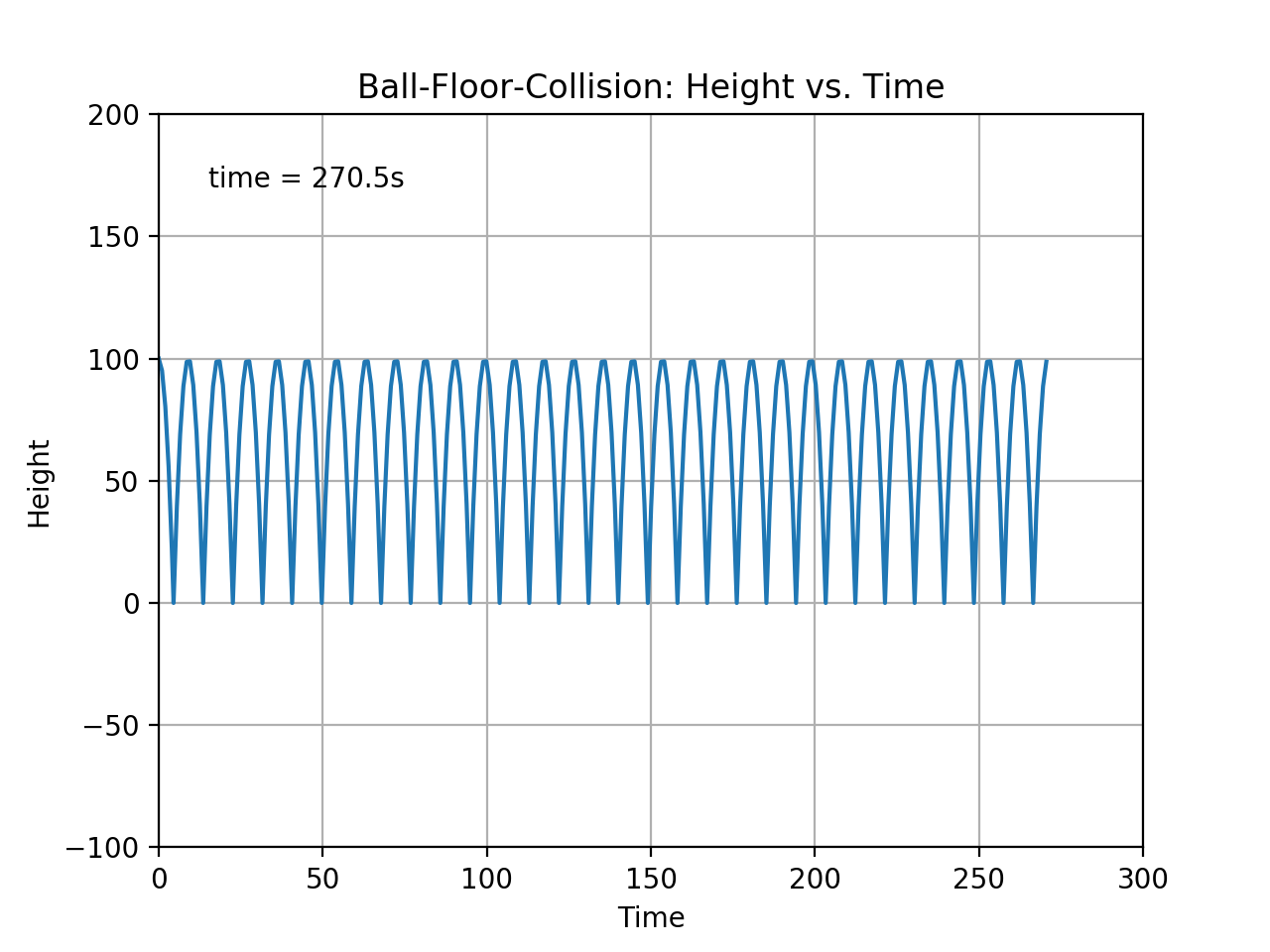
Using a small tolerance value prevents the ball from passing through the floor.
The primary function that you should focus on is
def respond_to_collision(self, state, t):
return [0, -1*state[1]], t"""
author: Faisal Z. Qureshi
email: faisal.qureshi@ontariotechu.ca
website: http://www.vclab.ca
license: BSD
"""
import numpy as np
from matplotlib import pyplot as plt
from matplotlib import animation
from scipy.integrate import ode
# Setup figure
fig = plt.figure(1)
ax = plt.axes(xlim=(0, 300), ylim=(-200, 1000))
plt.grid()
line, = ax.plot([], [], '-')
time_template = 'time = %.1fs'
time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes)
plt.title('Ball-Floor-Collision: Height vs. Time')
plt.xlabel('Time')
plt.ylabel('Height')
# Background for each function
def init():
line.set_data([], [])
time_text.set_text('')
return line, time_text,
# Called at each frame
def animate(i, ball):
line.set_xdata(np.append(line.get_xdata(), ball.t))
line.set_ydata(np.append(line.get_ydata(), ball.state[0]))
time_text.set_text(time_template % ball.t)
ball.update()
return line, time_text,
# Ball simulation - bouncing ball
class Ball:
def __init__(self):
# You don't need to change y, vy, g, dt, t and mass
self.state = [100, 0]
self.g = 9.8
self.dt = 1.0
self.t = 0
self.mass = 1
self.tol_distance = 0.00001
# We plan to use rk4
self.solver = ode(self.f)
self.solver.set_integrator('dop853')
self.solver.set_initial_value(self.state, self.t)
def f(self, t, y):
return [y[1], -self.g]
def is_collision(self, state):
return state[0] <= 0
def respond_to_collision(self, state, t):
# TO DO
return [0, -1*state[1]], t
def update(self):
new_state = self.solver.integrate(self.t + self.dt)
# Collision detection
if not self.is_collision(new_state):
self.state = new_state
self.t += self.dt
else:
state_after_collision, collision_time = self.respond_to_collision(new_state, self.t+self.dt)
self.state = state_after_collision
self.t = collision_time
self.solver.set_initial_value(self.state, self.t)
ball = Ball()
# blit=True - only re-draw the parts that have changed.
# repeat=False - stops when frame count reaches 999
# fargs=(ball,) - a tuple that can be used to pass extra arguments to animate function
anim = animation.FuncAnimation(fig, animate, fargs=(ball,), init_func=init, frames=300, interval=10, blit=True, repeat=False)
#plt.savefig('bouncing-ball-trace', format='png')
# Save the animation as an mp4. For more information, see
# http://matplotlib.sourceforge.net/api/animation_api.html
# anim.save('basic_animation.mp4', fps=30, extra_args=['-vcodec', 'libx264'])
plt.show()Extend this simulation to handle multiple balls falling from different heights with different initial velocities.
Via Canvas.