Fermat experiment

The goal of this exercise is to write a program that can compute the path of a ray of light as it passes through materials having different index of refraction.

The figure above illustrates this phenomenon. The ray of light bends as it enters the second medium. It turns out that by bending the ray of light takes the shortest amount of time to travel between point P and Q. The speed of light in a medium with index of refraction \(n\) is given by the following expression \[ v = \frac{c}{n}, \] where \(c\) is the speed of light in vacuum. The speed of light in vacuum is roughly \(1080\) million kilometers per hour.

Using the fact that the ray of light takes the shortest path (in time) when passing through materials having different index of refractions (see the figure below), find the actual path that the ray travels. We assume that the ray of light is initially traveling in vacuum and it exits in vacuum as well.

Code

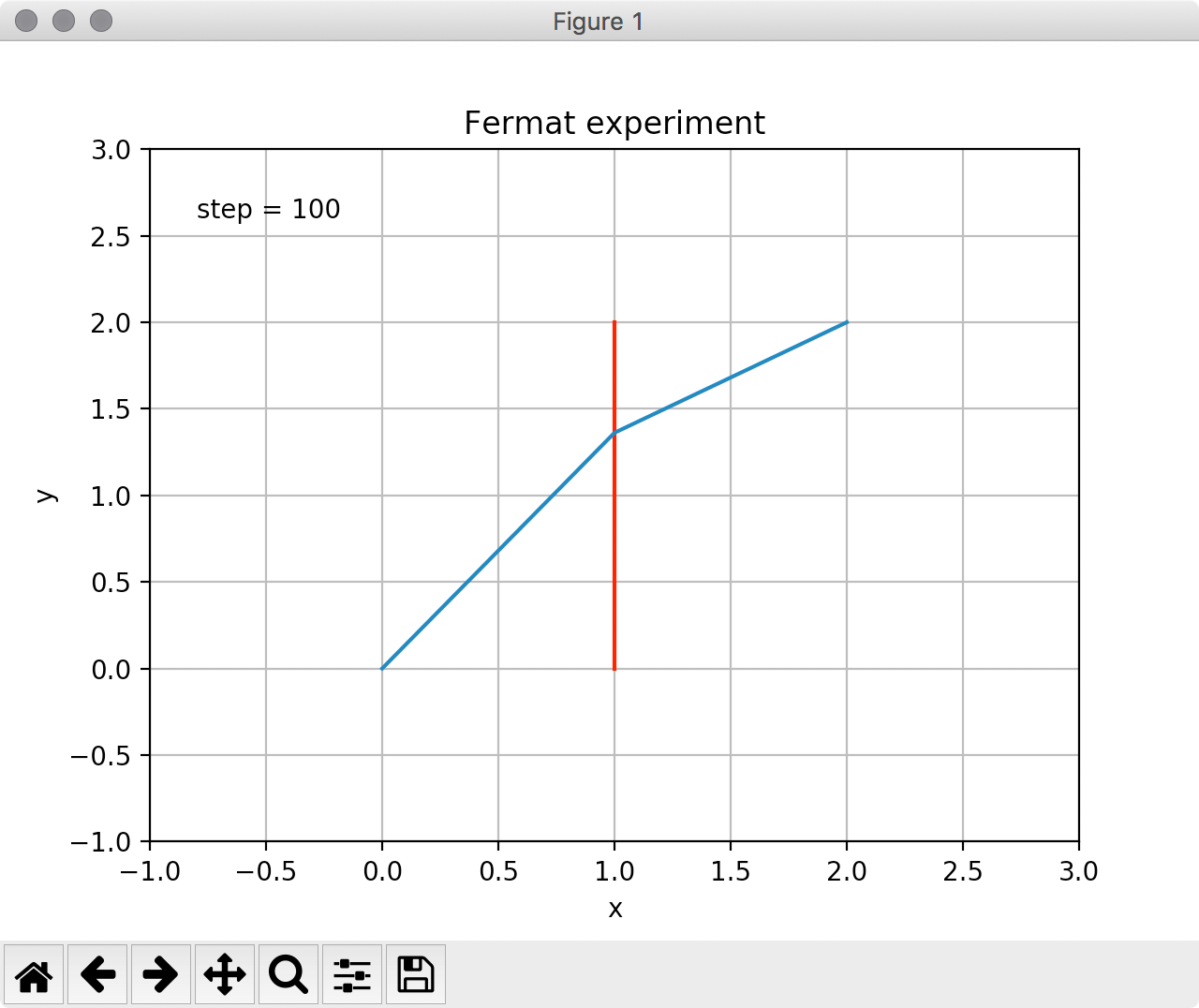
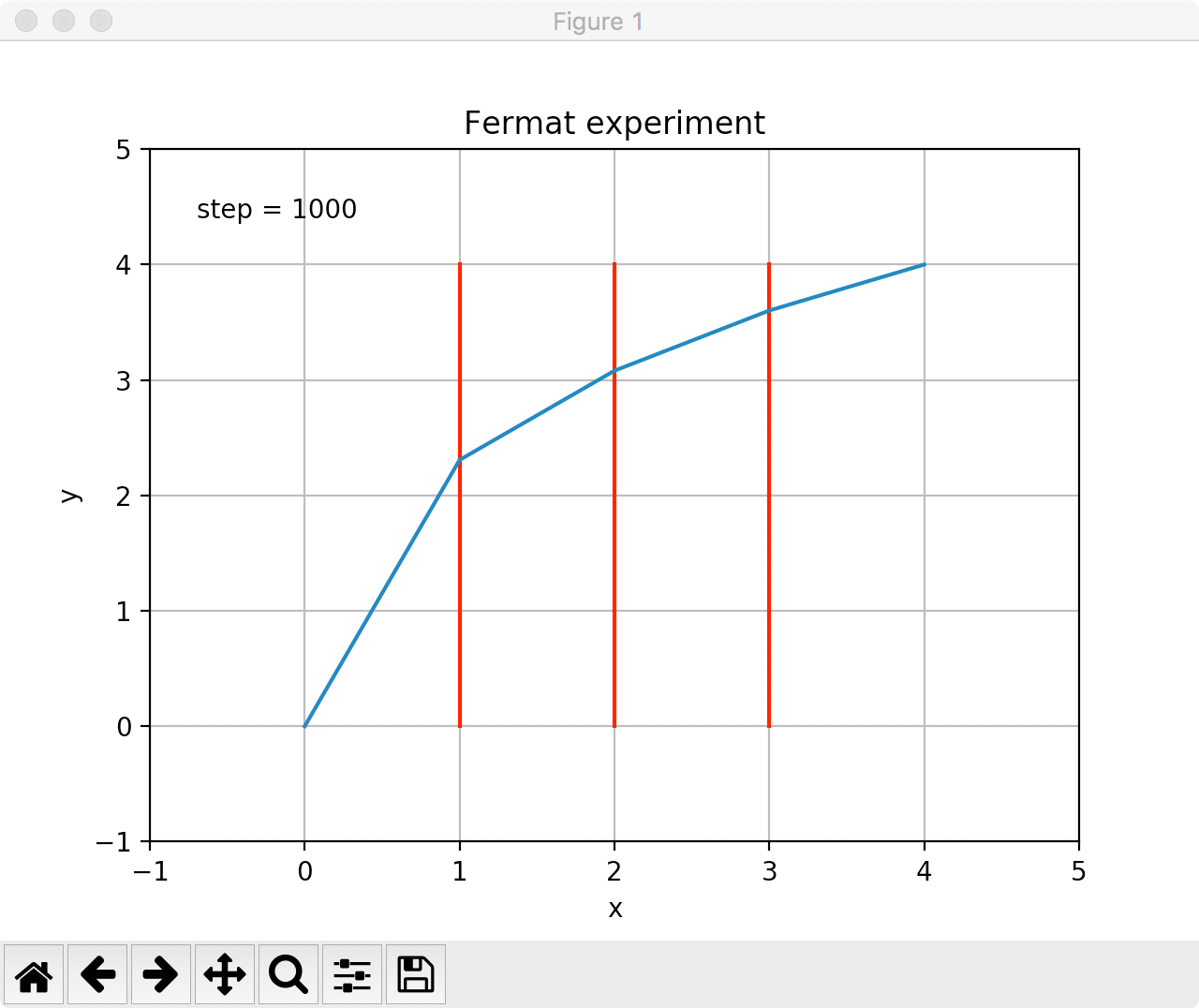
We will use the following class to set up the layers appropriately.

class Fermat:
    def __init__(self, N, dn):
        '''
        Sets up Fermat simulation -- light ray in media with different
        index of refractions

        N = number of media layers
        dn = change in index of refraction from one region to the next

        Layers are set at x-locations: 1, 2, 3, ..., N-1
        Starting x-location for the ray is 0
        Ending x-location for the ray is N
        Starting y-location for the ray is y[0]
        Ending y-location for the ray is y[N]
        Location of ray at layer i is y[i]
        Speed of light before layer i is v[i-1]
        '''
        self.dn = dn
        self.N = N
        self.y = np.empty((N+1)) # y coordinate of light ray, index is x coordinate
        self.v = np.empty((N))   # light speed of ray for medium starting at index value
        self.dy = 0.1            # max change in y at each step
        index_of_refraction = 1  # index of refraction for vacuum 
        self.steps = 0

        for i in range(N+1):
            self.y[i] = i
        for i in range(N):
            self.v[i] = 1. / index_of_refraction
            index_of_refraction += dn

The above piece of code sets up a material with N layers. v[0] represents the velocity in vacuum. v[1] onwards store velocities in different layers. y[0] and y[N] represent the entry and exit locations of the ray of light. We are interested in computing y[i] for \(i \in [1, N-1]\).

Starter code is available here.

Submission

The exercise will be completed in class. Be prepared to show your work to the instructor.