
Simulation and Modeling (CSCI 3010U)
Faculty of Science, Ontario Tech University
http://vclab.science.ontariotechu.ca
Discuss in class
Develop a simulation of a 2D ball bouncing off of a slanted floor as shown below.

For this simulation we assume the following:
Consider the figure shown below figure. \(\mathbf{i}\) represents the incoming direction. \(\mathbf{o}\) represents the outgoing direction. \(\mathbf{n}\) is the surface normal.
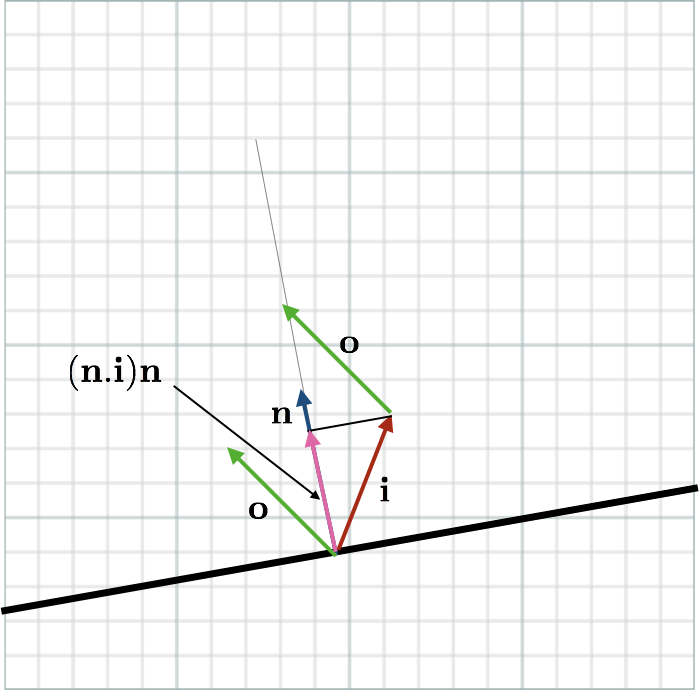
Notice that \[ 2 \mathbf{n} (\mathbf{i} . \mathbf{n}) = \mathbf{i} + \mathbf{o} \] Therefore, \[ \mathbf{o} = 2 \mathbf{n} (\mathbf{i} . \mathbf{n}) - \mathbf{i} \]
The exercise will be completed in class, and you do not need to submit anything. Be prepared to show your work to the instructor.
You can find starter code here.