
Homography¶
Faisal Qureshi
Professor
Faculty of Science
Ontario Tech University
Oshawa ON Canada
http://vclab.science.ontariotechu.ca
Copyright information¶
© Faisal Qureshi
License¶

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Lesson Plan¶
- Homography
- Homography application: Image stitching
- Solving for Homography
Homography¶
Projection of a point in a world plane to the image plane. The location of the point and that of its projection is related via homography.
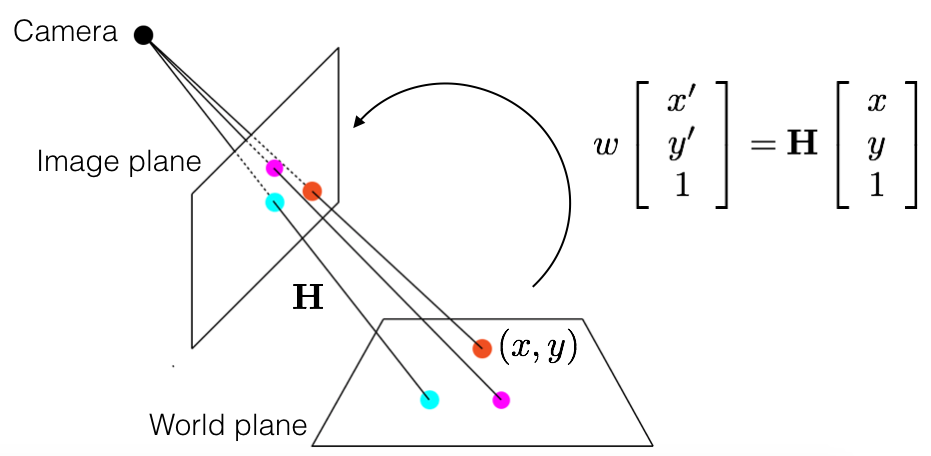
Generally speaking, points that lie on two planes are related via homography. This also means that the projections of points (that lie on a common plane) in two cameras are related via homography.
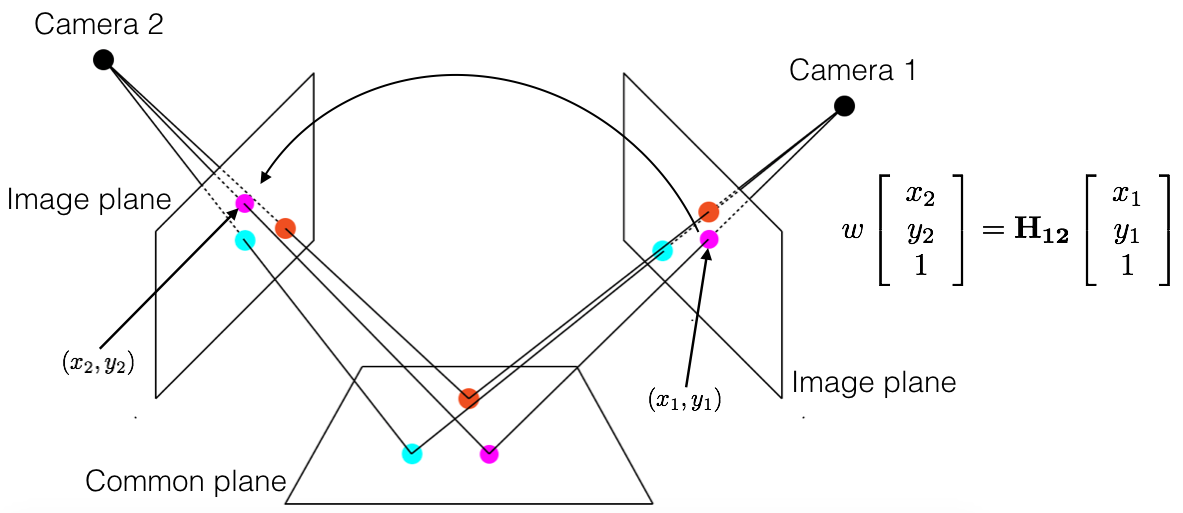
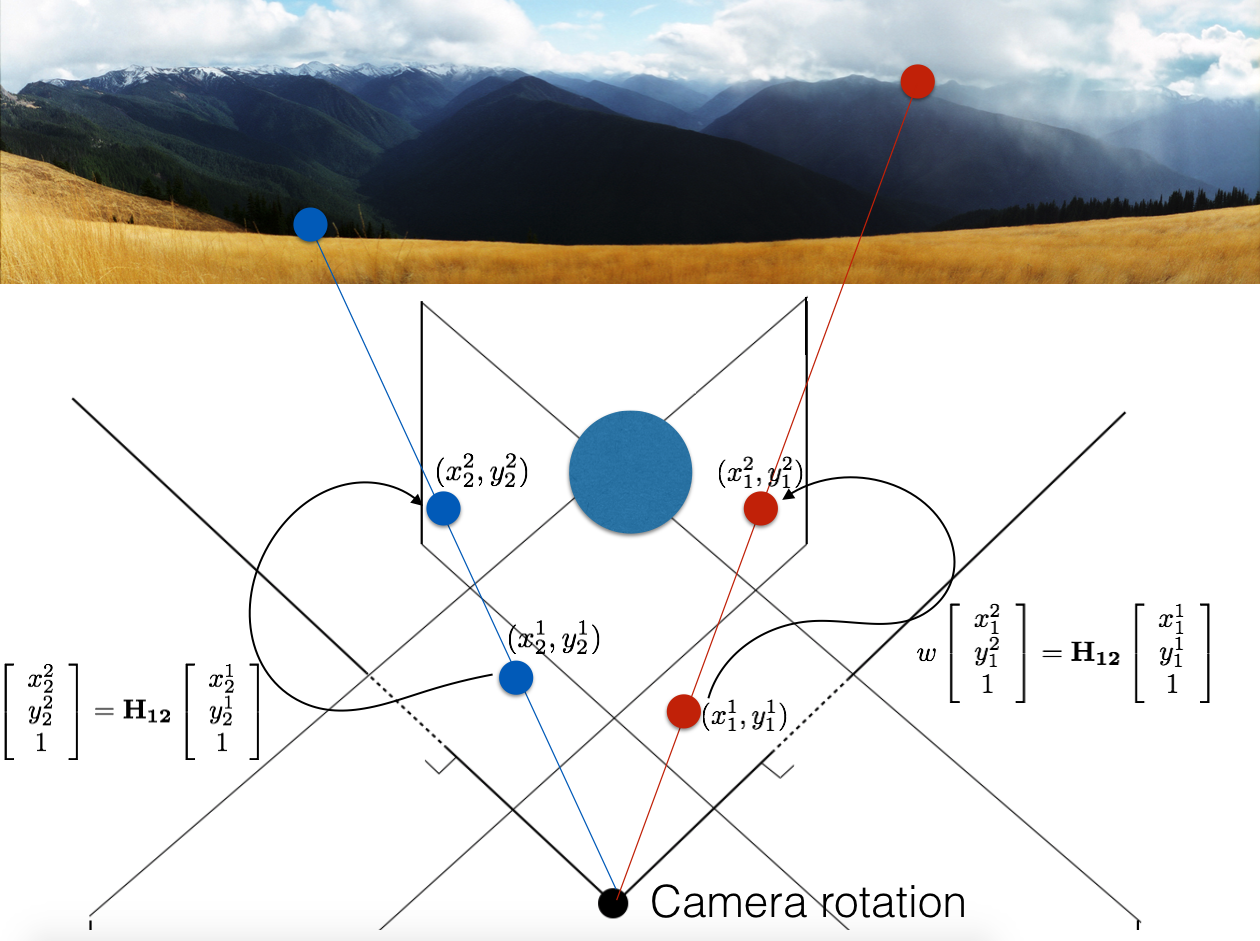
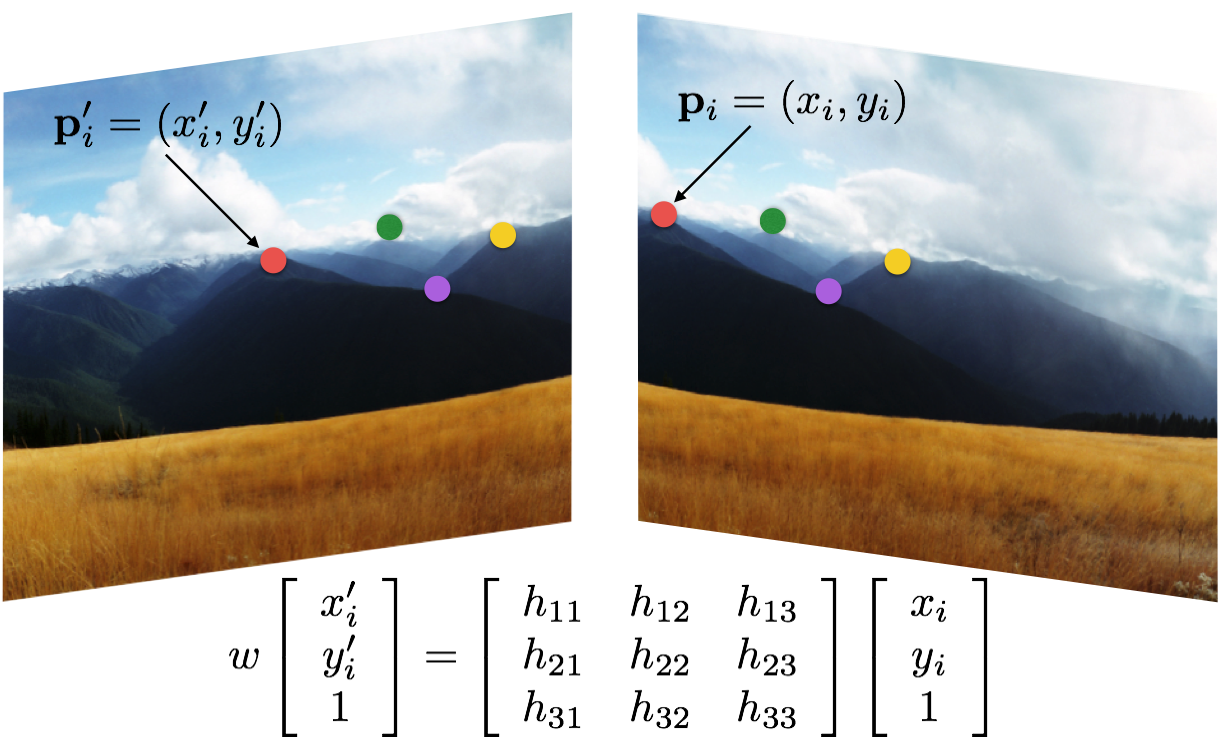
Image Stitching¶
Exercise 1¶
How many correspondences do we need to solve $\mathbf{H}$, where
$$ \mathbf{H} = \left[ \begin{array}{ccc} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \end{array} \right]. $$
Solution Exercise 1¶
This matrix can only be known upto a scale, so it has 8 degrees of freedom. We need at least 4 correspondences to solve this matrix.
This matrix often cannot be solved using pseudo-inverse technique due to numerical issues.
Solving for Homography¶
Re-write homography relationship as homogeneous equations
$$ \begin{align} x'_i &= \frac{h_{11} x_i + h_{12} y_i + h_{13}}{h_{31} x_i + h_{32} y_i + h_{33}} \\ y'_i &= \frac{h_{21} x_i + h_{22} y_i + h_{23}}{h_{31} x_i + h_{32} y_i + h_{33}} \end{align} $$
We can then write these as matrix-vector product
$$ \left[ \begin{array}{ccccccccc} x_i & y_i & 1 & 0 & 0 & 0 & -x_i x'_i & -y_i x'_i & - x'_i \\ 0 & 0 & 0 & x_i & y_i & 1 & -x_i y'_i & -y_i y'_i & - y'_i \end{array} \right] \left( \begin{array}{c} h_{11} \\ h_{12} \\ h_{13} \\ h_{21} \\ h_{22} \\ h_{23} \\ h_{31} \\ h_{32} \\ h_{33} \end{array} \right) = \mathbf{0} $$
Given $n$ point correspondences between two images, we set up $mathbf{A} \mathbf{x} = 0$ as follows:
$$ \begin{align} \left[ \begin{array}{ccccccccc} x_1 & y_1 & 1 & 0 & 0 & 0 & -x_1 x'_1 & -y_1 x'_1 & - x'_1 \\ 0 & 0 & 0 & x_1 & y_1 & 1 & -x_1 y'_1 & -y_1 y'_1 & - y'_1 \\ &&&&& \vdots &&& \\ x_i & y_i & 1 & 0 & 0 & 0 & -x_i x'_i & -y_i x'_i & - x'_i \\ 0 & 0 & 0 & x_i & y_i & 1 & -x_i y'_i & -y_i y'_i & - y'_i \\ &&&&& \vdots &&& \\ x_n & y_n & 1 & 0 & 0 & 0 & -x_n x'_n & -y_n x'_n & - x'_n \\ 0 & 0 & 0 & x_n & y_n & 1 & -x_n y'_n & -y_n y'_n & - y'_n \end{array} \right] \left( \begin{array}{c} h_{11} \\ h_{12} \\ h_{13} \\ h_{21} \\ h_{22} \\ h_{23} \\ h_{31} \\ h_{32} \\ h_{33} \end{array} \right) &= \mathbf{0} \\ \mathbf{A} \mathbf{x} & = \mathbf{0} \end{align} $$
$\mathbf{x}$ is the vector of unknowns.
Estimating $\mathbf{x}$¶
- Estimate using least-square fitting $$ \mathbf{x}^* = \underset{x}{\operatorname{argmax}} \| \mathbf{A} \mathbf{x} \|^2\ \mathrm{s.t.}\ \| \mathbf{x} \|=1 $$
- Note that the solution is also the right null-space of $\mathbf{A}$, so the solution is the eigenvector corresponding to the smallest eigenvalue of $\mathbf{A}^T \mathbf{A}$.
Image Stitching - Steps¶
Extract features

Find matches

Use RANSAC to estimate homography

Perform image stitching


